常见排序算法

常见排序算法

考点：

  • 各个排序算法的时间复杂度和空间复杂度的对比
  • 各个排序算法的基本思想和排序流程
  • 重点掌握快速排序、希尔排序和归并排序

排序算法对比：

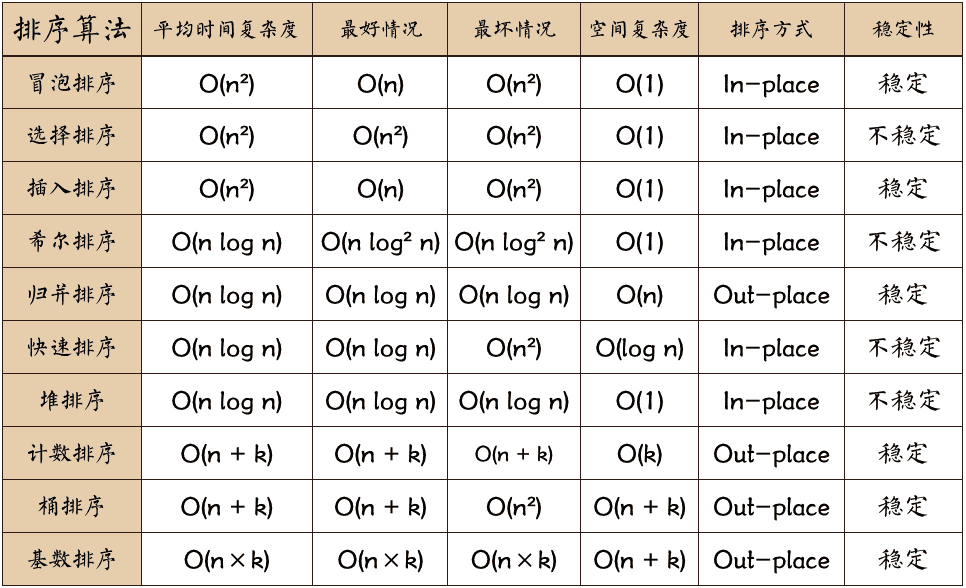
排序算法对比

学习资源推荐：

关于时间复杂度：

平方阶：插入排序、选择排序、冒泡排序

线性对数阶：快速排序、堆排序、归并排序

线性阶：基数排序、桶排序

关于稳定性：

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序

不稳定的排序算法：选择排序、快速排序、希尔排序、堆排序

总结：快速排序和希尔排序在排序速度上的表现比较优秀，而归并排序则稍微次之。

冒泡排序

基本思想：遍历要排序的数组，每次遍历时，它都会比较相邻两个数组元素的大小，如果前者比后者大，则交换它们的位置。一次遍历后，最大的元素会出现在数组末尾，重复上述操作，直到整个数组有序为止。

时间复杂度：O(N^2)

空间复杂度：O(1)

稳定性：稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
package org.example.sort;

import org.jetbrains.annotations.NotNull;

import java.util.Arrays;

public class BubbleSort {
    public static void main(String[] args) {
        int[] arr = {20, 40, 30, 10, 60, 50};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 冒泡排序
        bubbleSort(arr);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    public static void bubbleSort(@NotNull int[] arr) {
        int n = arr.length; // 数组长度
        boolean flag; // 标记
        for (int i = 0; i < n - 1; i++) {
            flag = false;
            for (int j = 0; j < n - i - 1; j++) {
                // 前者大于后者，交换位置
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    flag = true; // 发生了交换，则设置标记为 true
                }
            }
            if (!flag) {
                // 如果没有发生交换，则说明数组已经有序
                break;
            }
        }
    }
}

快速排序

基本思想：选择一个基准，将要排序的元素以基准为界，划分为两个部分，其中一部分的元素都比另一个部分的小，然后，再对这两个部分的元素分别进行快速排序（递归），最终得到有序的序列。

时间复杂度：最坏O(N^2)，平均O(NlogN)

空间复杂度：O(logN)

稳定性：不稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
package org.example.sort;

import java.util.Arrays;

public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {20, 40, 30, 10, 60, 50};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 快速排序
        quickSort(arr, 0, arr.length - 1);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    public static void quickSort(int[] arr, int left, int right) {
        if (left < right) {
            int pivot = arr[left];
            int i = left;
            int j = right;
            while (i < j) {
                // 从右向左找小于基准的元素
                while (i < j && arr[j] >= pivot) {
                    j--;
                }
                if (i < j) {
                    arr[i] = arr[j];
                }
                // 从左向右找大于基准的元素
                while (i < j && arr[i] <= pivot) {
                    i++;
                }
                if (i < j) {
                    arr[j] = arr[i];
                }
            }
            arr[i] = pivot;
            quickSort(arr, left, i - 1);
            quickSort(arr, i + 1, right);
        }
    }
}

插入排序

基本思想：将待排序的数组看作是两个数组，一个有序数组，一个无序数组，每次从无序数组中选择第一个元素，插入到有序数组的合适位置，重复上述操作即可完成排序。

时间复杂度：O(N^2)

空间复杂度：O(1)

稳定性：稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
package org.example.sort;

import org.jetbrains.annotations.NotNull;

import java.util.Arrays;

public class InsertSort {
    public static void main(String[] args) {
        int[] arr = {20, 40, 30, 10, 60, 50};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 插入排序
        insertSort(arr);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    public static void insertSort(@NotNull int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            for (int j = i; j > 0; j--) {
                if (arr[j] < arr[j - 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j - 1];
                    arr[j - 1] = temp;
                }
            }
        }
    }
}

希尔排序

基本思想：分组插入排序，对于待排序的数组，取一个 gap ，将数组中的元素分成若干个子序列，对每个子序列进行插入排序，然后缩小 gap，当 gap = 1 时，排序完成。

时间复杂度：-

空间复杂度：O(1)

稳定性：不稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
package org.example.sort;

import org.jetbrains.annotations.NotNull;

import java.util.Arrays;

public class ShellSort {
    public static void main(String[] args) {
        int[] arr = {20, 40, 30, 10, 60, 50};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 希尔排序
        shellSort(arr);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    public static void shellSort(@NotNull int[] arr) {
        int n = arr.length;
        for (int gap = n / 2; gap > 0; gap /= 2) {
            for (int i = 0; i < gap; i++) {
                for (int j = i + gap; j < n; j += gap) {
                    if (arr[j] < arr[j - gap]) {
                        int temp = arr[j];
                        int k = j - gap;
                        while (k >= 0 && arr[k] > temp) {
                            arr[k + gap] = arr[k];
                            k -= gap;
                        }
                        arr[k + gap] = temp;
                    }
                }
            }
        }
    }
}

选择排序

基本思想：从数组中找到最小的元素放到数组的起始位置，再从剩余的元素中找到最小的元素，放到已经排好序的数组末尾，重复上述流程，即可完成排序。

时间复杂度：O(N^2)

空间复杂度：O(1)

稳定性：不稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
package org.example.sort;

import java.util.Arrays;

public class SelectSort {
    public static void main(String[] args) {
        int[] arr = {20, 40, 30, 10, 60, 50};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 选择排序
        selectSort(arr);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    public static void selectSort(@NotNull int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            if (minIndex != i) {
                int temp = arr[minIndex];
                arr[minIndex] = arr[i];
                arr[i] = temp;
            }
        }
    }
}

堆排序

基本思想：堆排序是指利用堆这种数据结构设计的一种排序算法。

堆是一个近似完全二叉树的结构，分为最小堆和最大堆，最大堆通常被用来进行升序排序，而最小堆通常被用来进行降序排序。

时间复杂度：O(NlogN)

空间复杂度：O(1)

稳定性：不稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
package org.example.sort;

import org.jetbrains.annotations.NotNull;

import java.util.Arrays;

public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {20, 40, 30, 10, 60, 50};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 堆排序
        heapSort(arr);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    public static void heapSort(@NotNull int[] arr) {
        int len = arr.length;
        // 建立最大堆
        buildMaxHeap(arr, len);
        for (int i = len - 1; i > 0; i--) {
            swap(arr, 0, i);
            len--;
            heapify(arr, 0, len);
        }
    }

    private static void buildMaxHeap(@NotNull int[] arr, int len) {
        for (int i = (int) (double) (len / 2); i >= 0; i--) {
            heapify(arr, i, len);
        }
    }

    private static void heapify(@NotNull int[] arr, int i, int len) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;
        if (left < len && arr[left] > arr[largest]) {
            largest = left;
        }
        if (right < len && arr[right] > arr[largest]) {
            largest = right;
        }
        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, largest, len);
        }
    }

    private static void swap(@NotNull int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

归并排序

基本思想：长度为1的数组是有序，以此为递归边界，将数组一分为二，对两个部分分别进行归并排序，排序完成后，再合并这两个部分即可得到有序序列。

时间复杂度：O(NlogN)

空间复杂度：O(N)

稳定性：稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
package org.example.sort;

import org.jetbrains.annotations.NotNull;

import java.util.Arrays;

public class MergeSort {
    public static void main(String[] args) {
        int[] arr = {20, 40, 30, 10, 60, 50};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 归并排序
        mergeSort(arr, 0, arr.length - 1);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    private static void merge(@NotNull int[] arr, int left, int mid, int right) {
        int[] temp = new int[right - left + 1];
        int i = left, j = mid + 1, k = 0;
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        }
        while (i <= mid) {
            temp[k++] = arr[i++];
        }
        while (j <= right) {
            temp[k++] = arr[j++];
        }
        System.arraycopy(temp, 0, arr, left, temp.length);
    }

    public static void mergeSort(@NotNull int[] arr, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2;
            mergeSort(arr, left, mid);
            mergeSort(arr, mid + 1, right);
            merge(arr, left, mid, right);
        }
    }
}

桶排序

基本思想：将数组中的元素映射为桶的下标，遍历数组，每读取到一个元素，就让对应的桶加一，最后把桶中的数据提取出来，再转换成有序数组。

时间复杂度：最好情况为O(N + K)，最坏情况为O(N ^ 2)

空间复杂度：O(N + K)，N为数据规模，K为桶的个数

稳定性：稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
package org.example.sort;

import java.util.Arrays;

public class BucketSort {
    public static void main(String[] args) {
        int[] arr = {2, 4, 3, 1, 6, 5};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 桶排序
        bucketSort(arr, 10);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    public static void bucketSort(@NotNull int[] arr, int maxN) {
        int[] bucket = new int[maxN];
        for (int k : arr) {
            bucket[k]++;
        }
        for (int i = 0, j = 0; i < maxN; i++) {
            while (bucket[i] > 0) {
                arr[j++] = i;
                bucket[i]--;
            }
        }
    }
}

基数排序

基本思想：将整数按位数切割成不同的数字，然后按每个位数分别进行比较，从最低位开始依次进行排序，这样从最低位排序一直到最高位排序完成后，数组就变成了一个有序序列。

时间复杂度：O(N x K)

空间复杂度：O(N + K)

稳定性：稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
package org.example.sort;

import org.jetbrains.annotations.NotNull;

import java.util.Arrays;

public class RadixSort {
    public static void main(String[] args) {
        int[] arr = {53, 3, 542, 748, 14, 214, 154, 63, 616};
        System.out.println("排序前:");
        System.out.println(Arrays.toString(arr));
        // 基数排序
        radixSort(arr);
        System.out.println("排序后:");
        System.out.println(Arrays.toString(arr));
    }

    private static void radixSort(@NotNull int[] arr, int r) {
        int[] temp = new int[arr.length];
        int[] bucket = new int[10];
        for (int j : arr) {
            bucket[(j / r) % 10]++;
        }
        for (int i = 1; i < bucket.length; i++) {
            bucket[i] += bucket[i - 1];
        }
        for (int i = arr.length - 1; i >= 0; i--) {
            temp[bucket[(arr[i] / r) % 10] - 1] = arr[i];
            bucket[(arr[i] / r) % 10]--;
        }
        System.arraycopy(temp, 0, arr, 0, temp.length);
    }

    private static int getMaxValue(@NotNull int[] arr) {
        int result = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > result) {
                result = arr[i];
            }
        }
        return result;
    }

    public static void radixSort(@NotNull int[] arr) {
        int maxValue = getMaxValue(arr);
        for (int r = 1; maxValue / r > 0; r *= 10) {
            radixSort(arr, r);
        }
    }
}

参考资料

微信公众号

🎨 完整代码：https://github.com/liuyuhe666/sort

#算法 #排序
常见排序算法
https://liuyuhe666.github.io/2024/08/15/常见排序算法/
作者
Liu Yuhe
发布于
2024年8月15日
许可协议